在某些事物的發展呈現指數型(exponential)上升或下降時,我們可以用多項式回歸(Polynomial regression)模型來評估。比方說:原子彈爆炸威力、複利計算、熱能衰退等。這裡我們使用 Python 語言來完成多項式回歸模型的訓練與回歸。
1. 讀取資料
先觀察資料
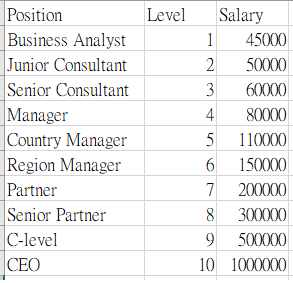
這是一筆職位、職級與薪水的對照資料。目前看起來, 特徵資料在 column0 , column1,預測資料在最後方
這裡還是跟以前一樣,利用來讀取 CSV 檔案
dataset = pd.read_csv('Position_Salaries.csv')
對於特徵資料,column 0 只是職位名稱,還不算是數字資料。因此由 column 1 開始 取資料。
X= dataset.iloc[:,1:-1].values
預測資料在最後方的整行
y= dataset.iloc[:,-1].values
2. 創造線性模型
還是利用 LinearRegression 這個 class
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)
3. 導入多項式特徵
最後的結果是結合 線性方程式和多項式矩陣。
先引用多項式特徵 class
from sklearn.preprocessing import PolynomialFeatures
用這個 class 得到多項式
poly_reg=PolynomialFeatures(degree=2)
這裡用 degree=2 指定一個 2 次方的多項式
接下來我們將特徵值帶入多項式,得到 2 次方的多項式特徵陣列
X_poly=poly_reg.fit_transform(X)
建立一個線性回歸模型 lin_reg_2
lin_reg_2=LinearRegression()
最後就是用這個 2 次方的多項式特徵陣列 X_poly 來訓練這個線性回歸模型 lin_reg_2
lin_reg_2.fit(X_poly, y)
4. 視覺化模型輸出
4.1 先看原始資料與預測模型的關係圖
X 是檔案裏面原始的資料, lin_reg 是線性回歸模型
plt.scatter(X, y, color='red')
plt.plot(X, lin_reg.predict(X), color='blue')
plt.title('Truth or Bluff : Linear Regression')
plt.xlabel('Position Level')
plt.ylabel('Salary')
plt.show()
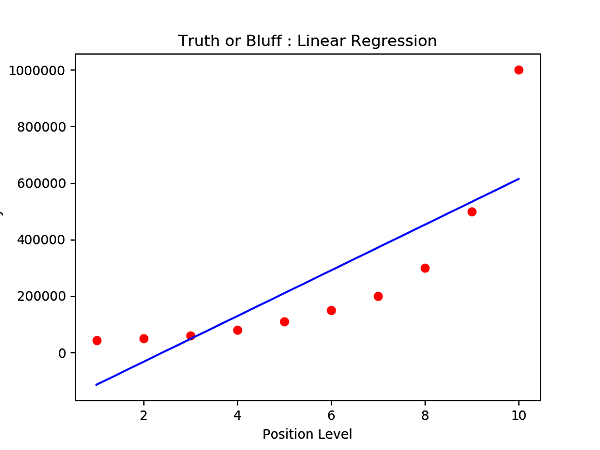
看起來,線性模型並不符合資料集合的預測
現在我們用多項式模型來試試看:
plt.scatter(X, y, color='red')
plt.plot(X, lin_reg_2.predict(X), color='blue')
plt.title('Truth or Bluff : Linear Regression')
plt.xlabel('Position Level')
plt.ylabel('Salary')
plt.show()
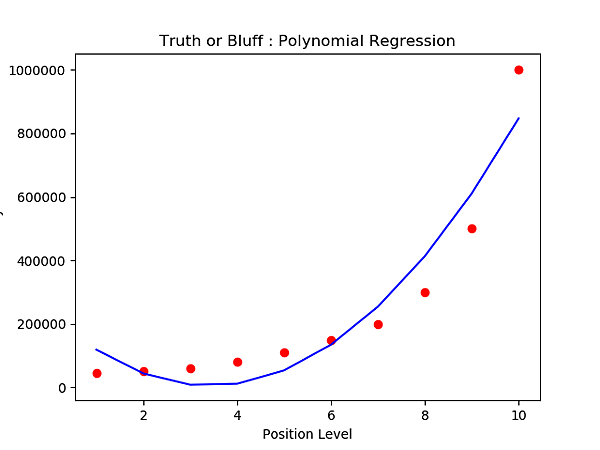
看起來的結果明顯比線性要好!
目前的多項式模型只用到 2 次方;如果用更高階呢?
我們將 poly_reg=PolynomialFeatures(degree=2)
degree 改成 4,再來看一下:
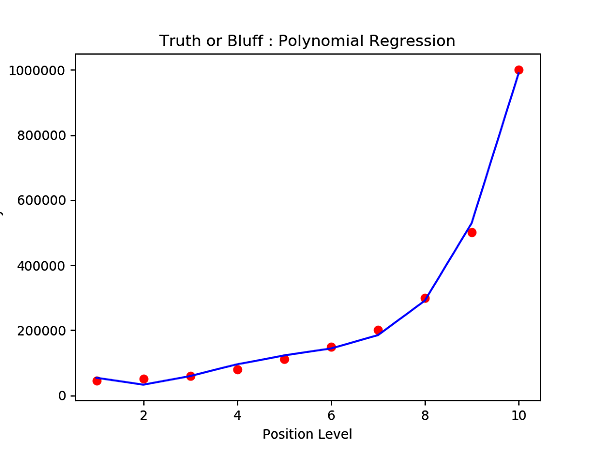
這次的結果又比上次更接近了!
結論
對於具有指數型發展的數據,我們可以利用多項式回歸模型來趨近或模擬。
