某些自然界事物的發展呈現指數型(exponential)上升或下降時,我們可以用多項式回歸(Polynomial regression)模型來評估。比方說:原子彈爆炸威力、複利計算、熱能衰退等。這裡我們使用 R 語言來完成多項式回歸模型的訓練與回歸。
讀取 CSV 檔案資料

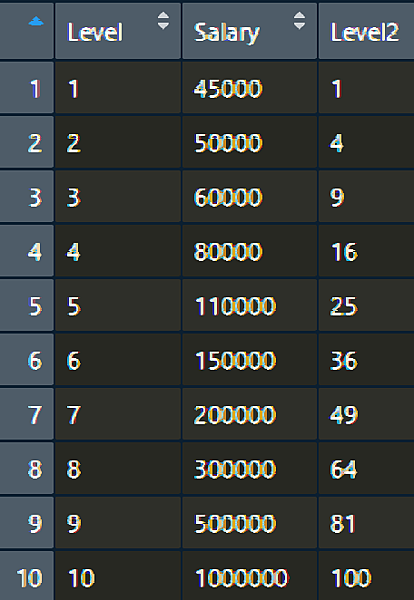
右上方的全域資料顯示一個變數 dataset,有10筆資料,每筆資料有 3 行
在這個區域直接按兩下,左上方的區域就顯示資料內容。
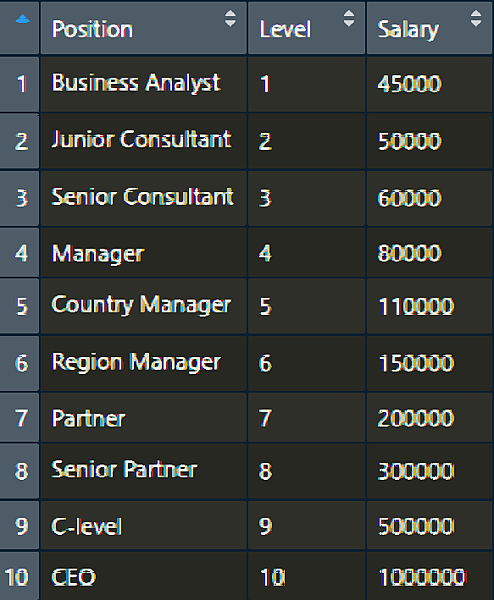
看一下這筆資料。除了職位(Position)之外,等級(Level)和薪水(Salary) 都是數值資料。目前看起來應該是等級越高,薪水也越高。這裡我們用多項式回歸(Polynomial regression)模型來訓練。
將等級(Level)和薪水(Salary)資料取出:
dataset= dataset[2:3]
右上方的全域資料就改成 dataset,有10筆資料,每筆資料有 2 行

在這個區域直接按兩下,左上方的區域就顯示資料內容。
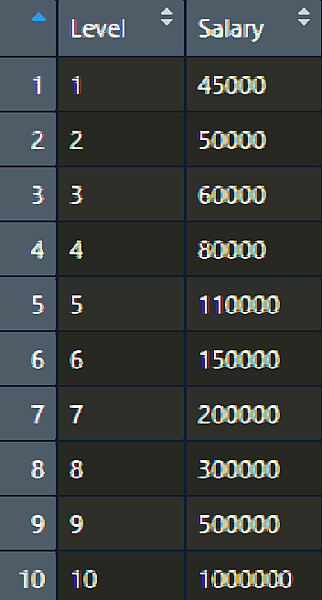
在這裡,等級(Level)是獨立變數(independent variable),而薪水(Salary)是相依變數(dependent variable)
為了和多項式回歸模型作比較,我們先建立一個線性回歸模型
lin_reg=lm(formula = Salary .,
data=dataset)
執行這行後,在右上方就出現 lin_reg 這個變數
在左下方執行區也看到

在左下方執行區 下 summary 命令

就可以看到線性回歸模型訓練後的參數
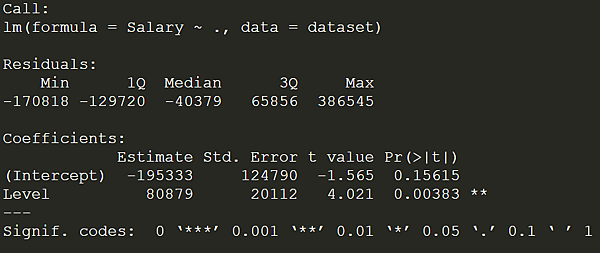
這裡可以看到,Level 有2顆星,表示具有顯著性
多項式回歸表示在資料裡有次方的運算。
這裡我們先假設 等級(Level)的平方與薪水(Salary)相關
這裡為了計算與資料顯示的方便,我們先在資料裡面多加一行(Column)
在 R 語言裡面,多加一行的資料很簡單:這裡我們先加一行 等級2(Level2),它來自於等級(Level)的平方數值:
datasetLevel2=datasetLevel2
執行後,我們在資料裡可以看到多了一行 等級2(Level2) 的資料
,數值是 等級(Level)的平方數值
接下來,建立多項式回歸(Polynomial regression)模型和線性模型的語句是一樣的:
Poly_reg=lm(formula = Salary .,
data=dataset)
也可以多加一個3次方的項目
datasetLevel3=datasetLevel3
執行後,我們再用 summary() 來看模型參數
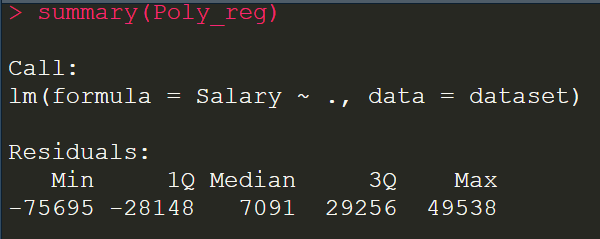
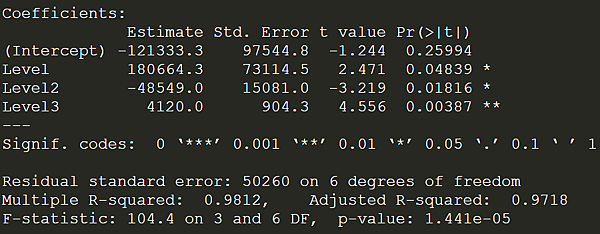
視覺化繪圖
現在我們可以用繪圖函式庫來描繪出模型的輸出結果。
用 ggplot2
使用時:library(ggplot2)
ggplot() + geom_point(x=,y=)
橫軸 x 是 等級(Level)是獨立變數(independent variable),而薪水(Salary)是相依變數(dependent variable)。因此這裡寫:
geom_point(x=datasetLevel,y=datasetSalary)
用紅色來描出圖點:
color='red') +
geom_point(x=datasetLevel,y=datasetSalary),
color='red')
第三部分是預測數值
geom_line(x=datasetLevel,y=),
color='blue')
第一個,先把顏色改成藍色 color='blue'
第二個,再把 y 軸改成預測值
直接用函式 predict()
先放 線性回歸模型 lin_reg,後放 輸入資料 dataset
y=predict(lin_reg ,newdata = dataset)
+ ggtitle('Linear Regression')
+ xlab('Level') + ylab('Salary')
執行後可看到右下方的繪圖結果:
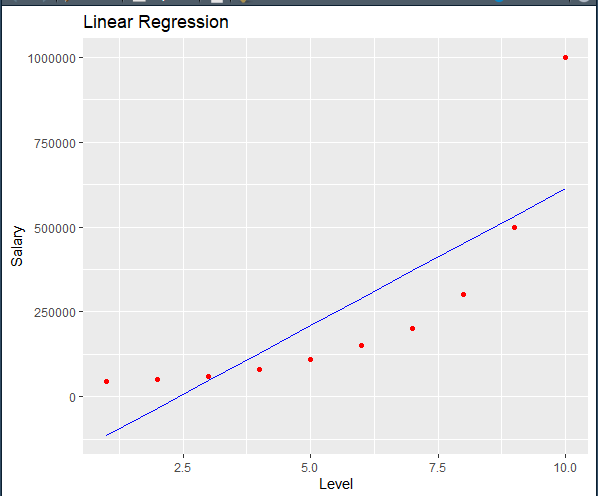
然後是多項式模型的預測結果
ggplot() +
geom_point(aes(x=datasetLevel,y=datasetSalary),color='red')+
geom_line(aes(x=datasetLevel,y=predict(Poly_reg,newdata=dataset)),color='blue')+
ggtitle('Polynomial Regression')+ xlab('Level')+ ylab('Salary')
只有把模型改換和標題的字串內容改掉而已。
執行後可以有這樣的結果:
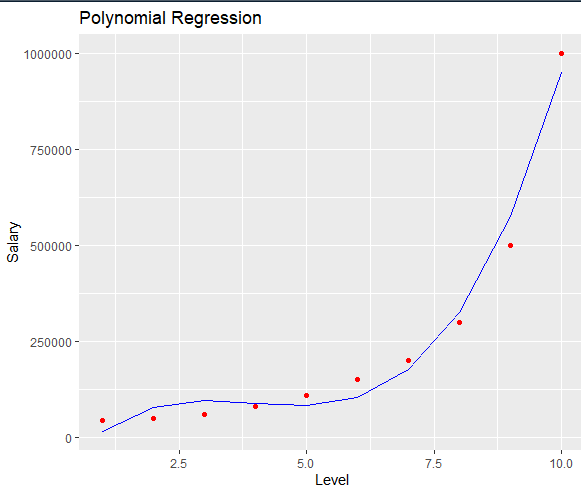
看起來比直線線性回歸的模型更接近紅色的等級(Level)!
目前是利用 3 次方的多項式來逼近,如果要利用4次方呢?
很簡單,只要再增加一個行(Column)
datasetLevel4=datasetLevel4
執行這行指令,可看到 dataset 多增加一行
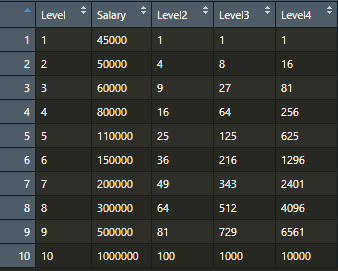
再執行一次多項式模型的訓練:
Poly_reg=lm(formula = Salary .,
data=dataset)
再繪圖一次
ggplot() +
geom_point(aes(x=datasetLevel,y=datasetSalary),color='red')+
geom_line(aes(x=datasetLevel,y=predict(Poly_reg,newdata=dataset)),color='blue')+
ggtitle('Polynomial Regression')+ xlab('Level')+ ylab('Salary')
就有一張新的逼近圖
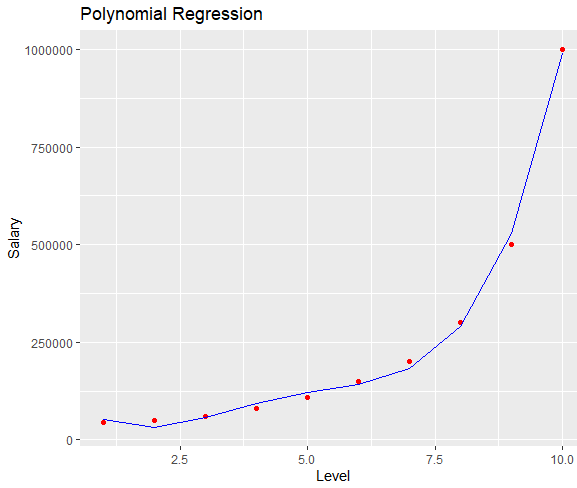
比較預測誤差
要比較模型預測值,要先取得模型輸出預測值
,前面在繪圖的部分我們已經看過,就是用 predict() 函式。
這裡在 dataset Level 裡面 有 6 和 7,如果要預測一個不存在的數字 6.5 呢?
可以用以下的語句:
y_pred=predict(lin_reg,data.frame(Level=6.5))
我們在右上方可以看到線性回歸模型的預測結果:

330379 在 Level 裡面 6 和 7 中間好像沒有比較符合。那我們再用多項式模型來預測
程式大部分都相同,只要改2個地方
1. 模型代號改成 Poly_reg
2. data.frame(Level=6.5 再增加其他次方的數據
在 dataset 裡面我們只增加 6和7 的 24 次方,卻沒有 6.5 的 24 次方。這裡預測就需要手動加上去:
y_pred2=predict(Poly_reg,data.frame(Level=6.5,
Level2 = 6.52,
Level3 = 6.53,
Level4 = 6.54))
執行後可以看到預測結果:
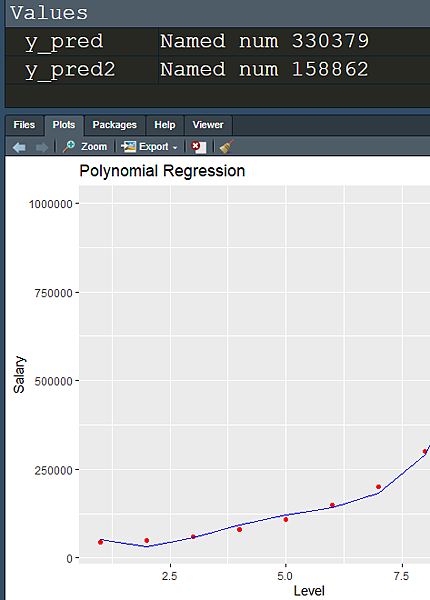
預測值是 158862 跟線性回歸模型比起來比較接近數據資料!
